Pull Requests to Tomorrow Jamie Kang's weblog on computing

Auto-Encoding Variational Bayes

21 May 2017 | PR12, Paper, Machine Learning, Generative Model, Unsupervised Learning

흔히 VAE (Variational Auto-Encoder)로 잘 알려진 2013년의 이 논문은 generative model 중에서 가장 좋은 성능으로 주목 받았던 연구입니다. Ian J. Goodfellow의 “GAN”을 이해하려면 필수적으로 보게 되는 논문이기도 합니다.

이 논문은 수학식이 중심이라 이해하기가 쉽지 않습니다만, 다행히 그동안 많은 분들이 해오신 풀이가 이미 있기 때문에 이번 포스팅에서는 가급적 그림과 개념적인 이해 중심으로 설명하겠습니다.

Introduction

Generative Model

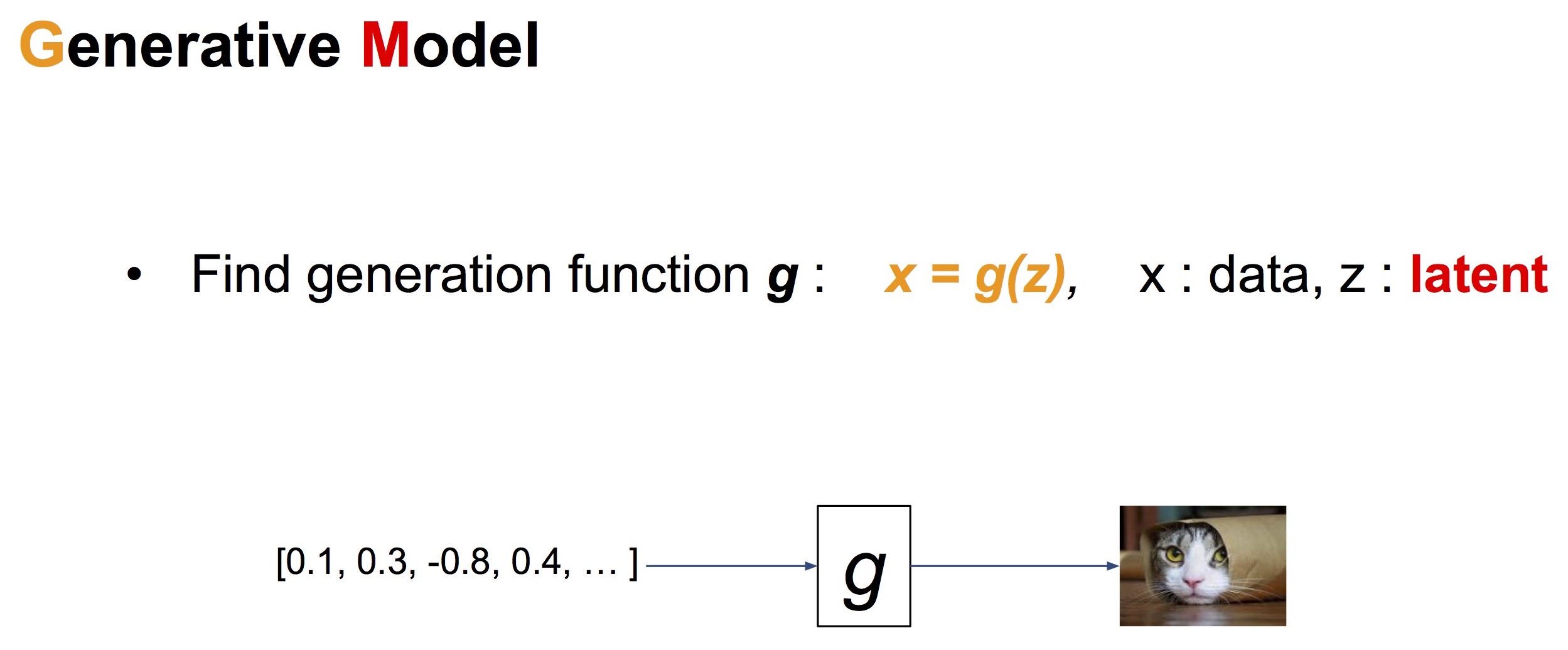
이 논문에서 소개할 Variational Auto-Encoder는 일종의 Generative Model입니다. Generative Model은 입력 변수(latent variable) $z$로부터 결과물 $x$ (가장 흔하게는 image)을 만들어내는 모델입니다. 아래 그림과 다음 그림은 김남주 님의 슬라이드 “Generative Adversarial Networks (GAN)”에서 인용했습니다.

Generative Model

Unsupervised learning과 generative model을 비교하면 아래 표와 같습니다.

model formula distribution role
unsupervised model $z = f(x)$ $p(z|x)$ Encoder
generative model $x = g(z)$ $p(x|z)$ Decoder

Autoencoder

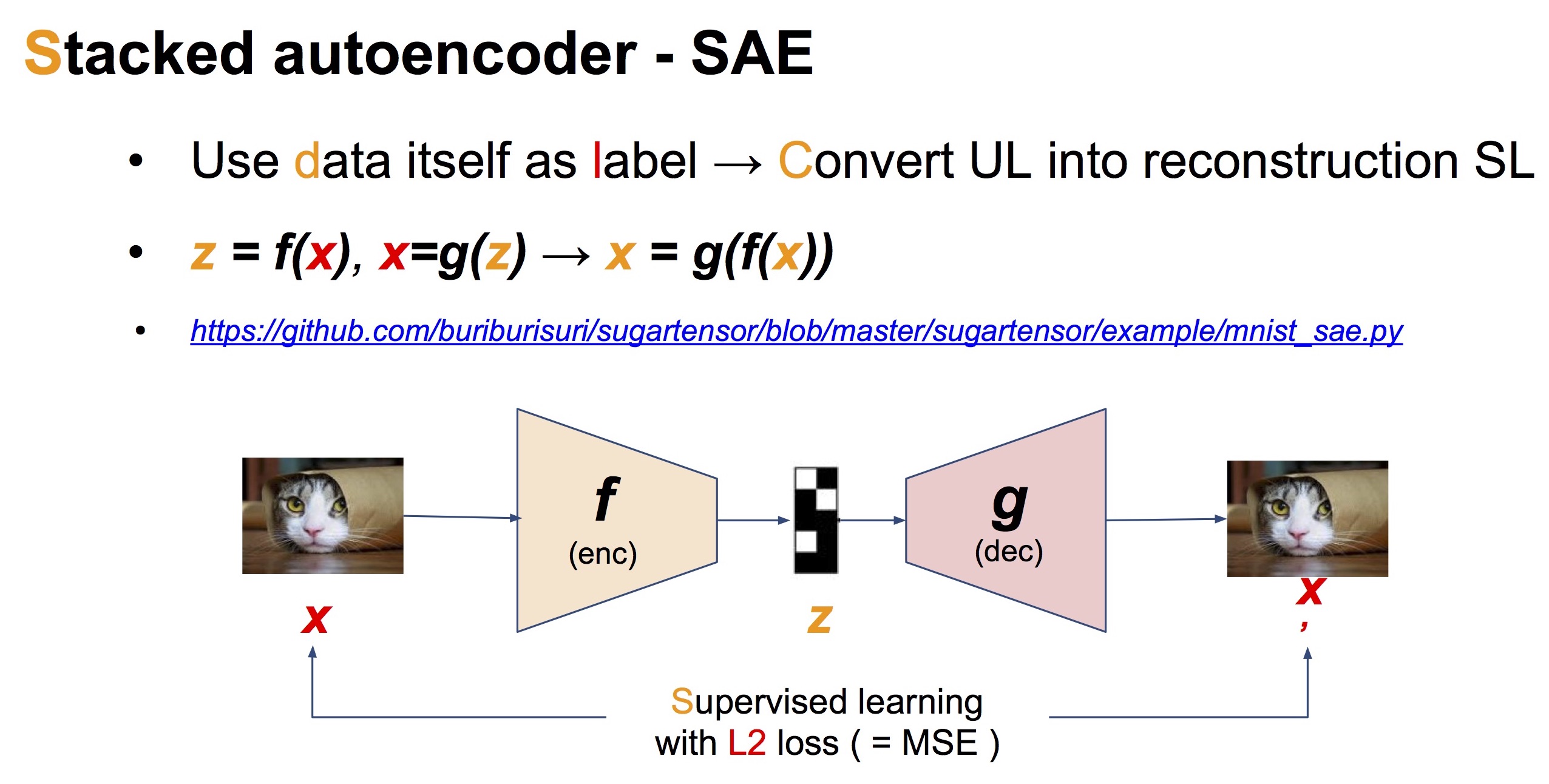
Autoencoder는 입력 데이터 $x$ 자신을 다시 만들어내려는 neural network 모델입니다. 구조는 아래 그림처럼 latent code $z$를 만드는 encoder와 $x’$를 만드는 decoder가 맞붙어 있는 형태가 됩니다. Autoencoder는 입력 $x$와 출력 $x’$ 사이의 L2 loss (= mean squared error)를 최소화하도록 training 됩니다.

Stacked Autoencoder

Variational Auto-Encoder (VAE)

VAE는 Autoencoder의 특성을 물려 받았지만, 약간 다른 점이 있습니다.

  • Autoencoder에서는 $z$가 training data와 특별히 관련이 없이 단순히 계산 중간에 나오는 deterministic한 값일 뿐입니다. 반면, VAE에서는 latent variable $z$가 continuous한 분포를 가지는 random variable이라는 점이 중요한 차이입니다. 이 latent variable $z$의 분포는 training 과정에서 data로부터 학습됩니다.

  • VAE는 decoder 부분만 떼어내 Generative Model로 사용할 수 있습니다. Encoder는 decoder에 어떤 입력 $z$를 넣을지 학습으로 알게 됩니다.

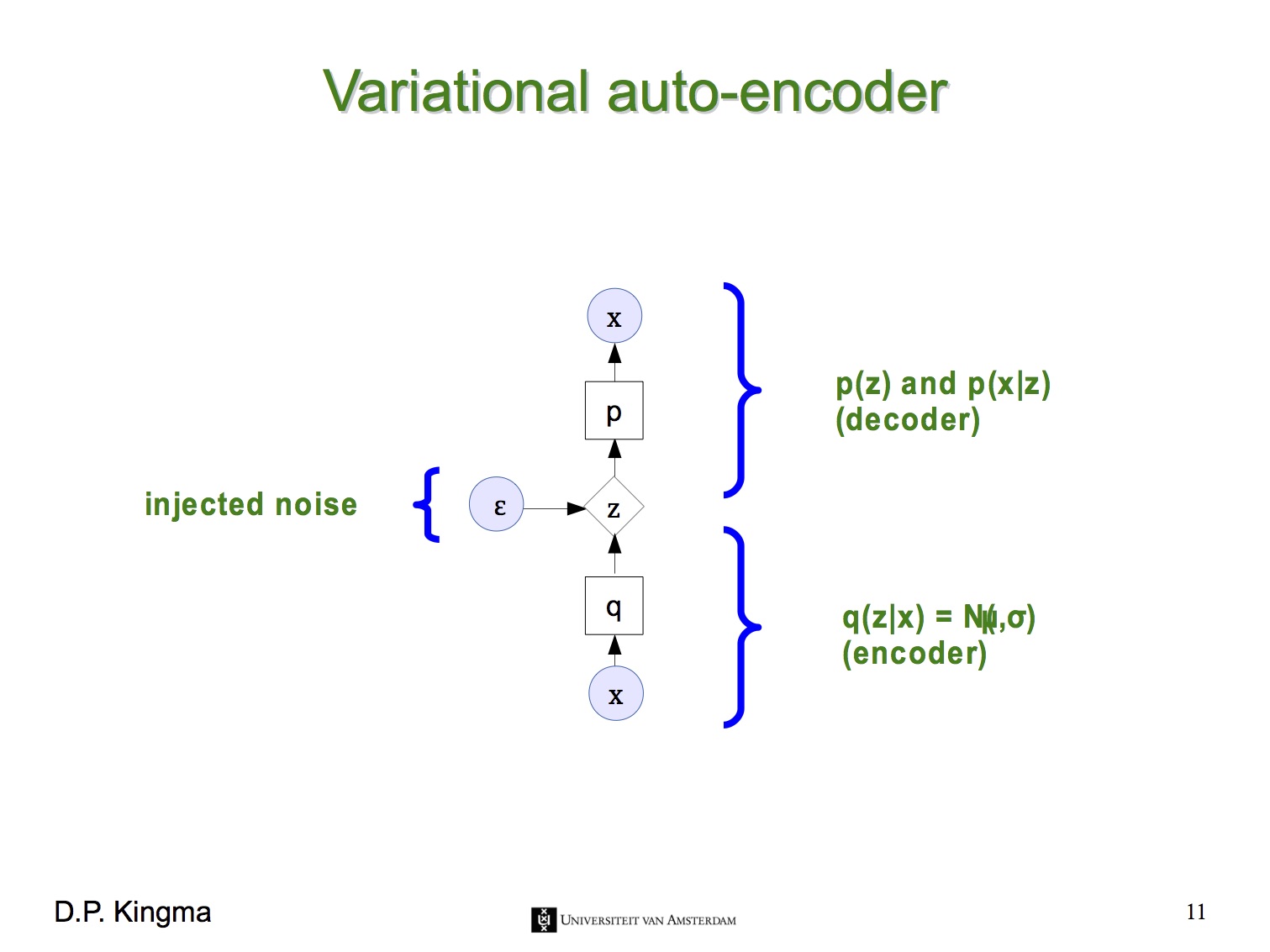
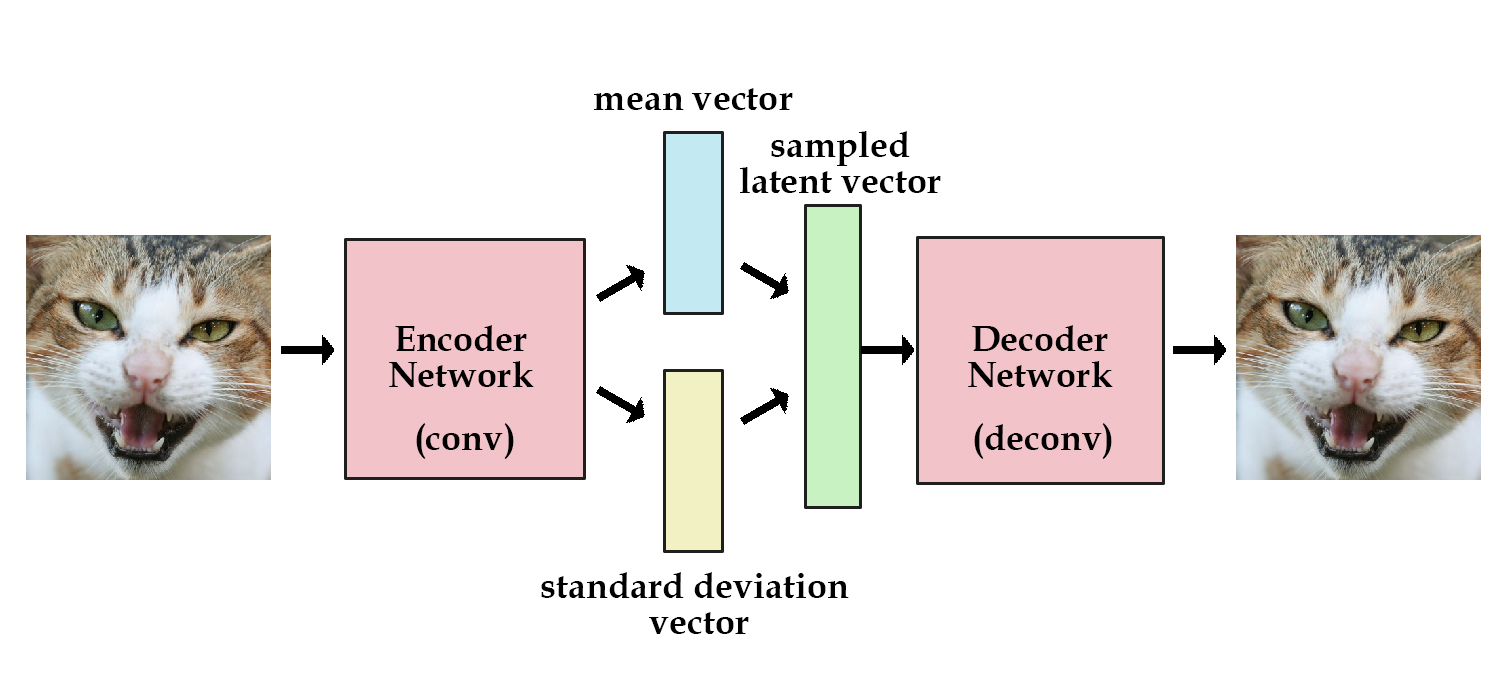
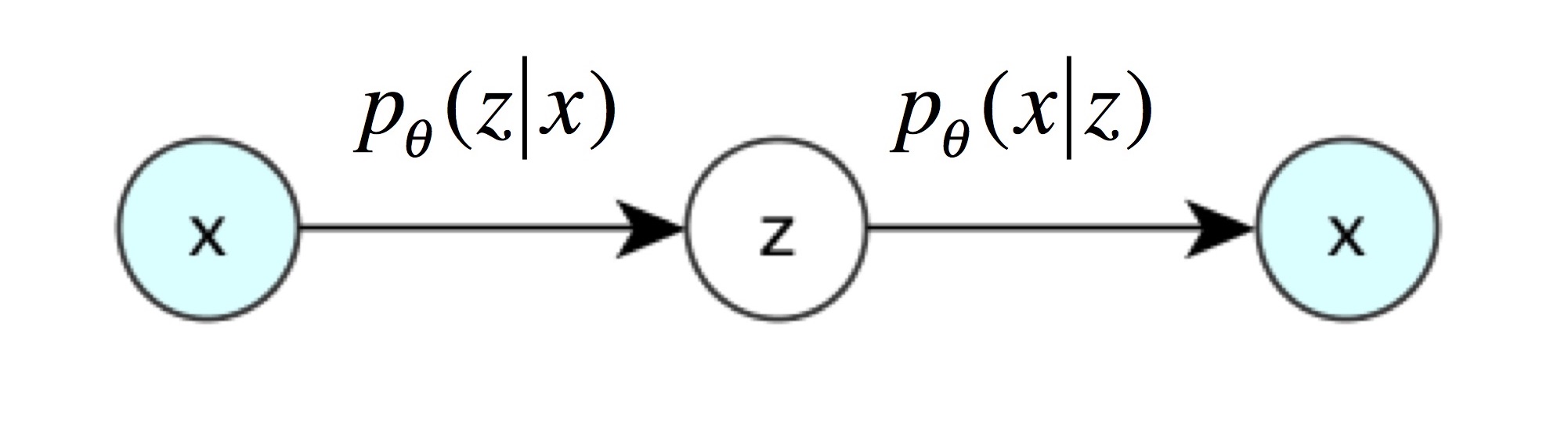
즉, 지금부터는 latent variable $z$가 평균과 표준편차로 결정되는 확률 분포를 가진다는 뜻입니다. VAE의 encoder는 주어진 $x$로부터 $z$를 얻을 확률 $p(z|x)$로, VAE의 decoder는 $z$로부터 $x$를 얻을 확률 $p(x|z)$로 나타낼 수 있습니다. 아래 그림들은 Kevin Frans의 블로그와 Oliver Dürr의 슬라이드에서 인용했습니다.

krfrans-vae durr-pp18

Decoder

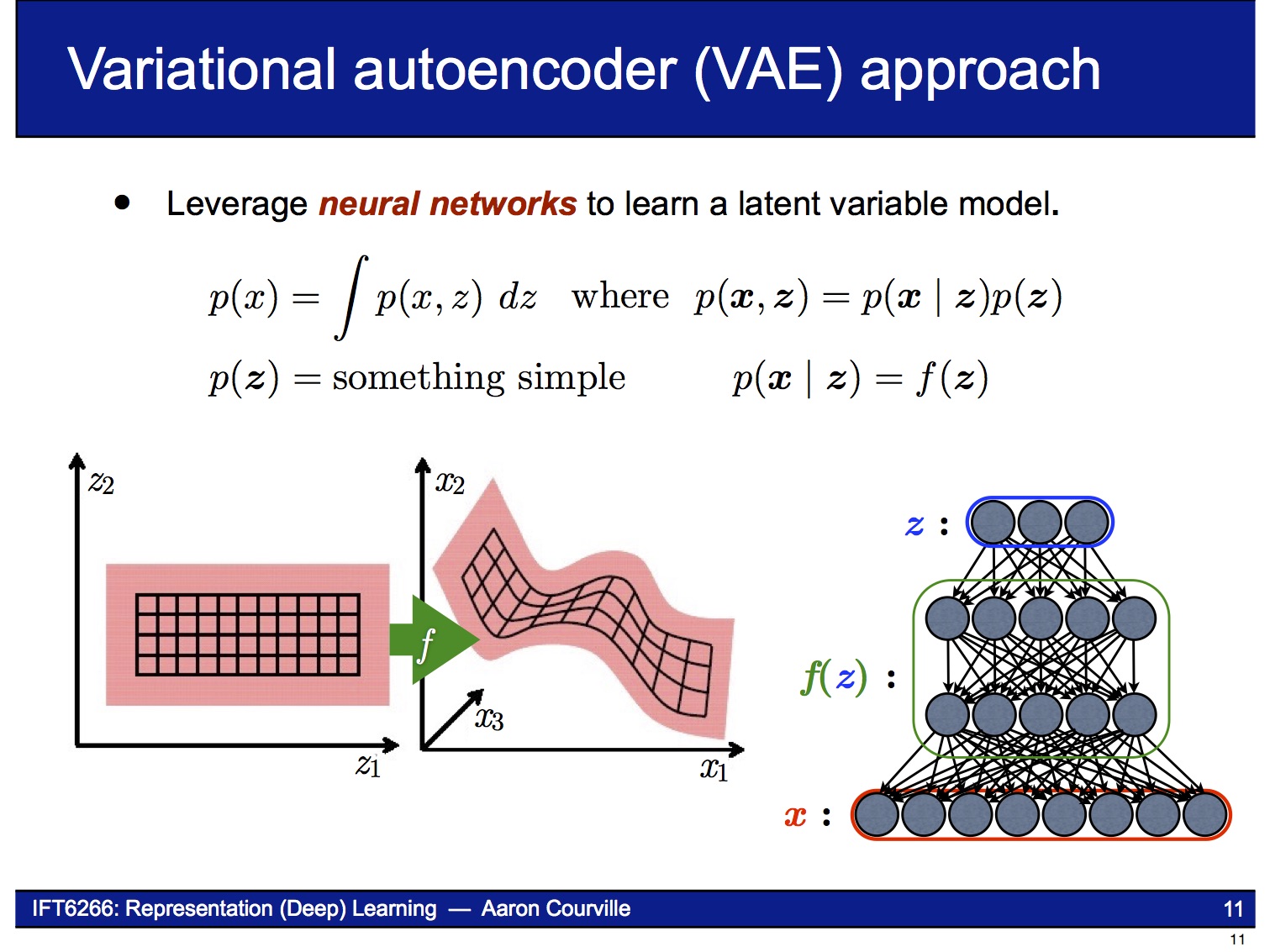
VAE의 decoder는 latent variable $z$로부터 $x$를 만들어내는 neural network입니다. 결과물 $x$의 확률 분포 $p(x)$를 알기 위해, decoder는 $p(x|z)$을 학습합니다. 아래에 나오는 슬라이드들은 이 논문의 저자인 Kingma의 발표자료에서 인용했습니다.

kingma-pp4

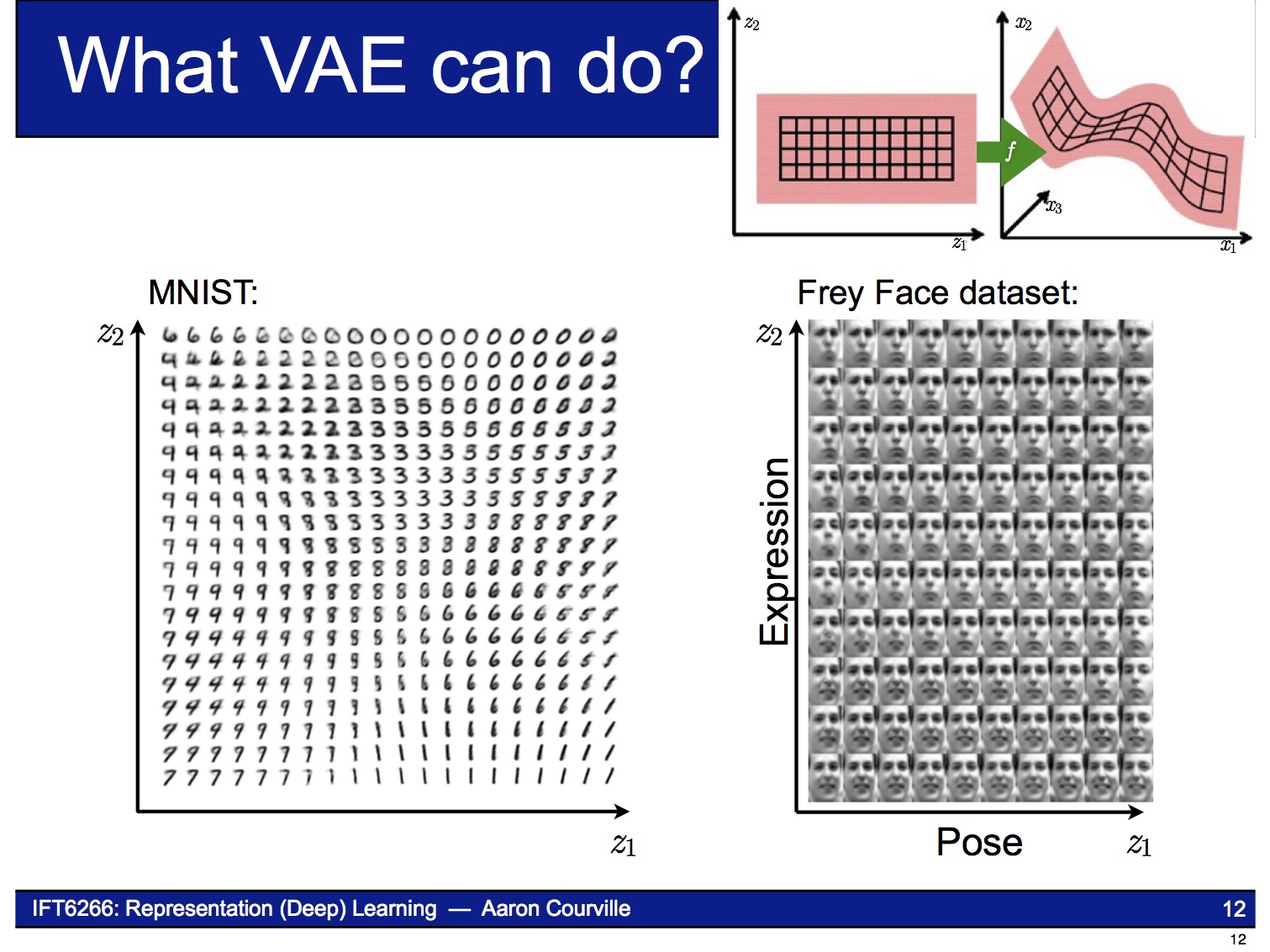
Decoder는 Generative Model이므로 latent variable $z$의 sample 값이 달라짐에 따라 아래 그림처럼 연속적으로 변하는 결과물을 만들어낼 수 있습니다.

kingma-pp5

Encoder

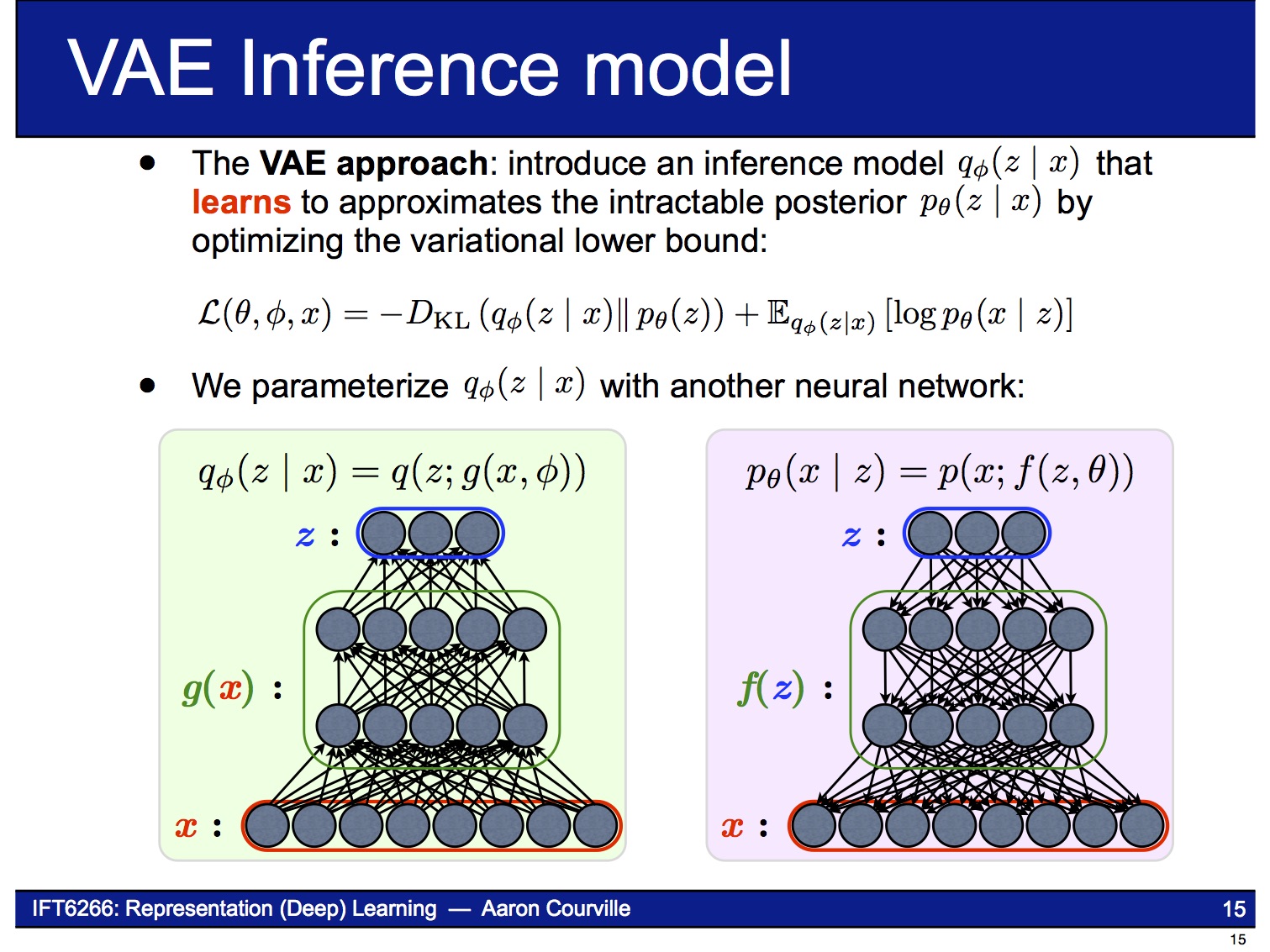
VAE의 encoder는 주어진 $x$로부터 $z$를 얻는 neural network입니다. VAE 논문에 나오는 복잡한 수학식들은 바로 이 encoder 부분을 설명하기 위한 것입니다. $x$가 주어졌을 때 $z$의 확률 분포 $p(z|x)$는 posterior distribution이라고 불리는데, 그 값을 직접 계산하기 어려운(intractable) 것으로 알려져 있습니다.

그래서 이 논문에서는 계산할 수 있는 $q(z|x)$라는 변수를 대신 도입해 $p(z|x)$로 근사 시키는 방법을 사용합니다. 이런 방법을 Variational Bayesian methods 또는 Variational Inference라고 부르고, VAE의 ‘Variational’도 거기에서 온 것입니다. (수식에 나오는 $\theta$, $\phi$는 각각 $p(z|x)$, $q(z|x)$의 parameter입니다.)

우리가 알고 싶은 것은 실제 데이터의 확률 분포인 $p(x)$이지만, 계산의 편의를 위해 log likelihood 값인 $\log p(x)$를 대신 풀어보면 lower bound 를 얻을 수 있습니다.

이제 파라미터 $\phi$와 $\theta$를 조절하여 를 maximize하는 점을 찾으면, 그때 $\log p(x)$와 이 같아질 것으로 생각할 수 있습니다.

kingma-pp13

Maximize하는 문제라면 neural network를 만들어서 gradient-ascent 알고리즘으로 풀 수 있습니다. 그런데, 한 가지 문제가 있습니다.

Decoder에 latent variable $z$를 넣으려면 $z$가 random variable이므로 sampling을 해야하는데, sampling은 미분 가능하지가 않아서 gradient를 구할 수 없습니다.

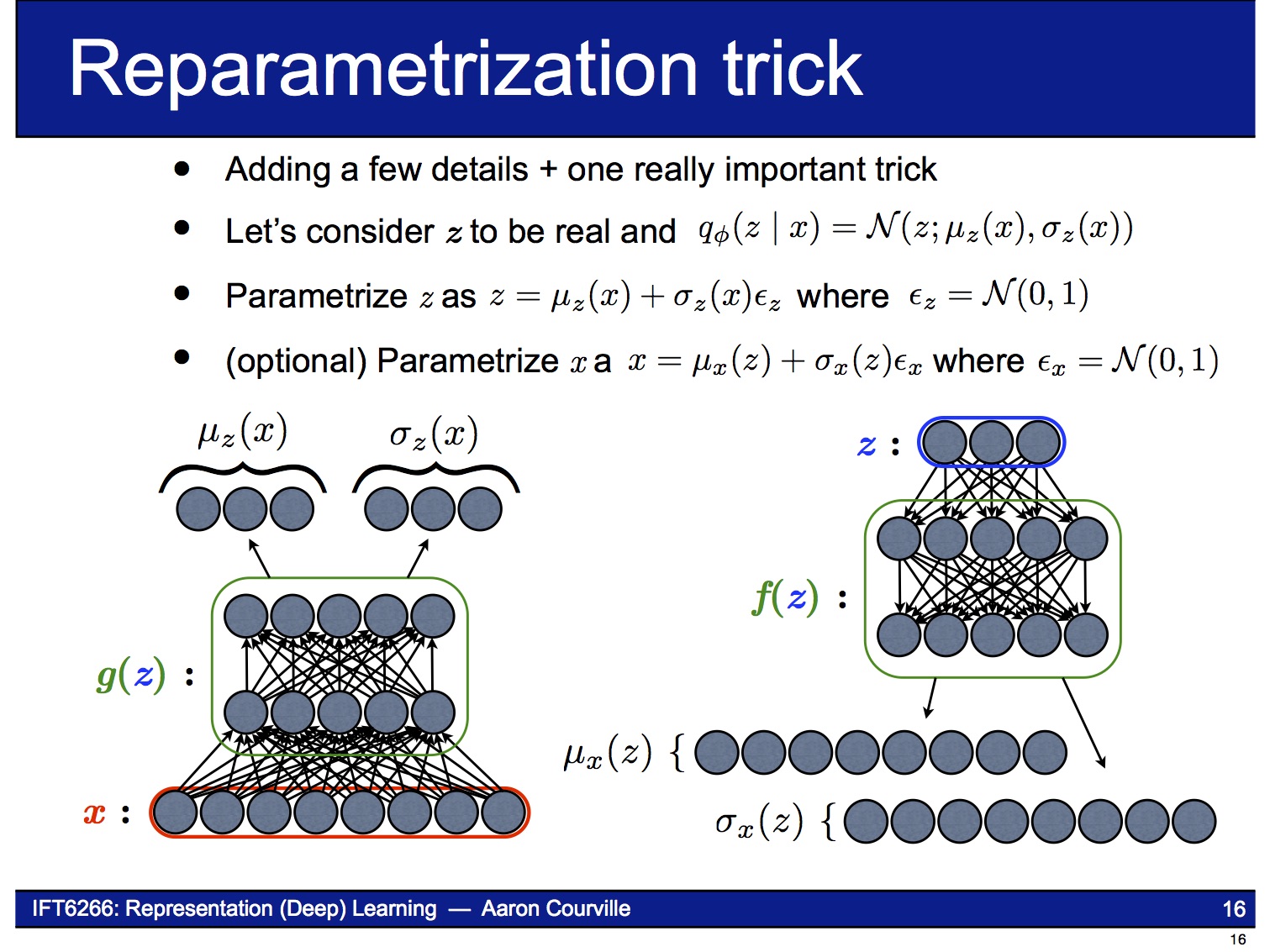
이 문제를 해결하기 위해 reparameterization trick이라는 기법을 사용합니다. 이 기법은 $z$의 stochastic한 성질을 마치 자기 자신은 deterministic한데 외부에서 random noise $\epsilon$이 입력되는 것처럼 바꿔 버립니다. 즉 이제 VAE는 parameter $\phi$ (= $\mu_z (x)$, $\sigma_z (x)$)에 대해 end-to-end로 미분 가능한 시스템이 됩니다.

kingma-pp15 kingma-pp18

Putting it all together

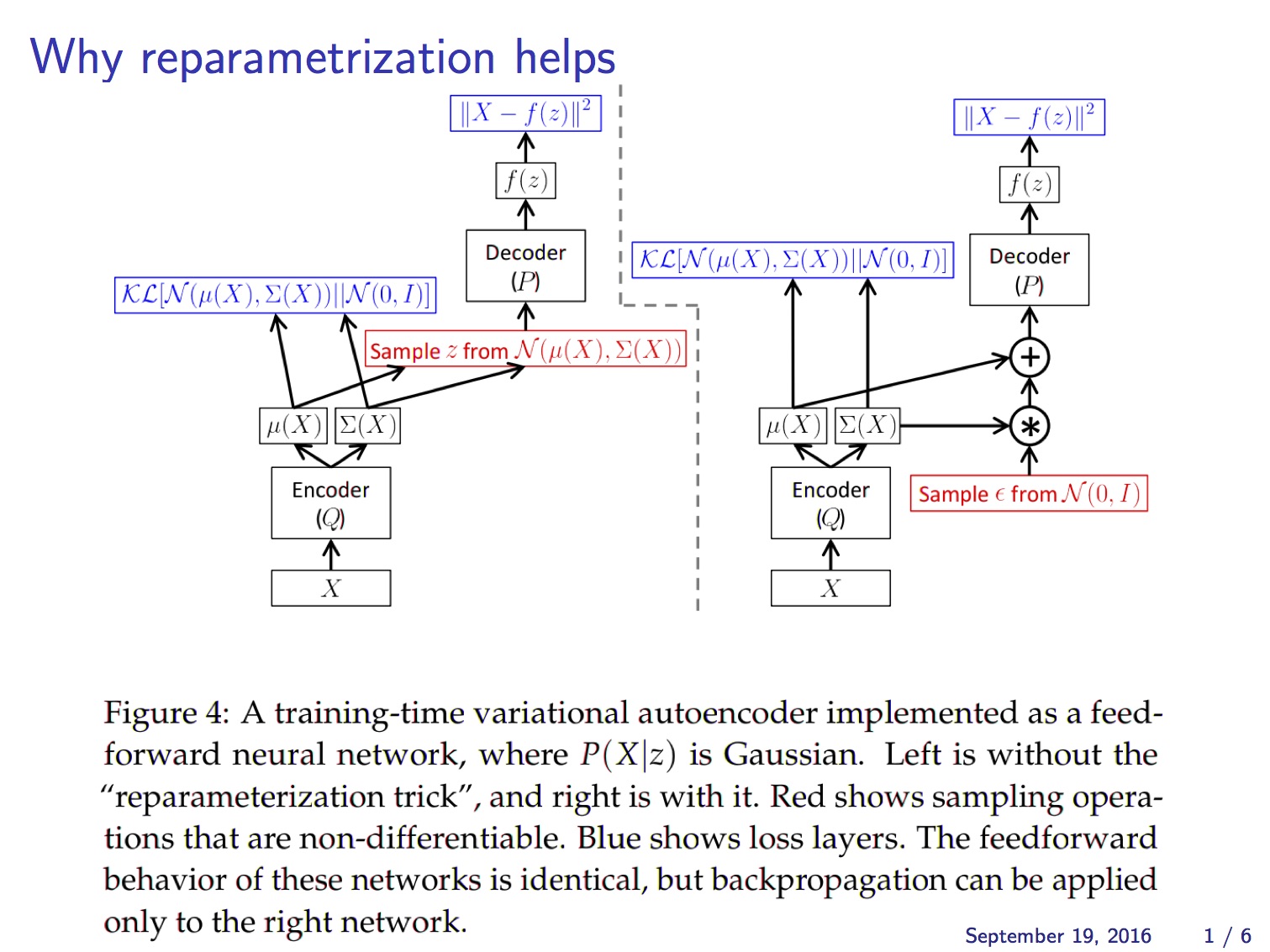
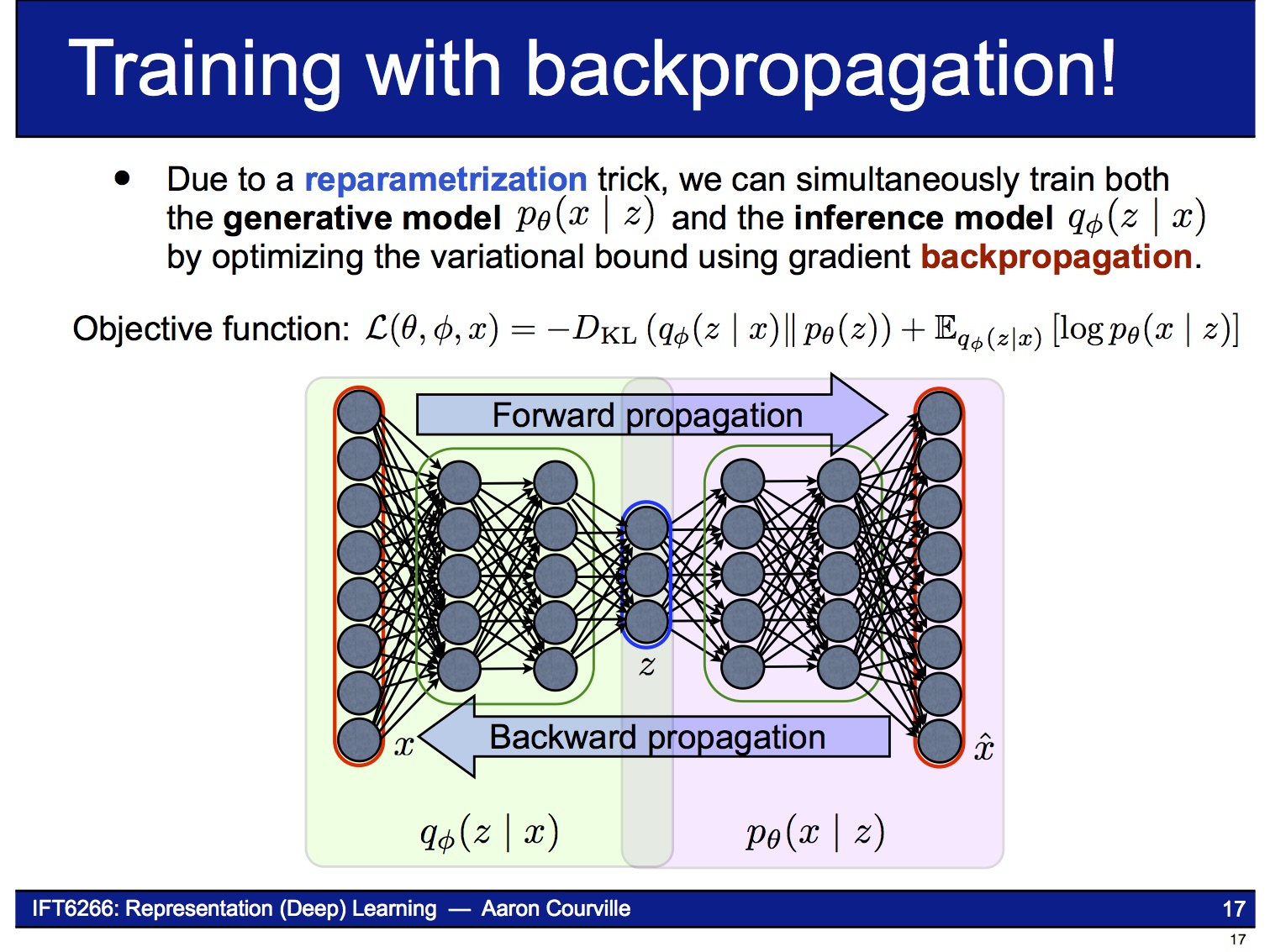
아래 그림은 앞에서 설명한 reparameterization trick을 반영해서 VAE의 구조를 다시 그린 것입니다.

kingma-pp17

즉 이제 VAE는 end-to-end로 미분 가능한 시스템이 되어 backpropagation을 사용하여 gradient-ascent 문제를 풀 수 있습니다. 이때 object function은 앞의 (2)식에서 보인 가 됩니다.

kingma-pp19

(2)식의 의 RHS에서 첫 번째 항에 나오는 KL-divergence $\cal{D}_{KL}(q(z|x)||p(z))$는 적절한 가정을 하면 아래와 같이 analytic하게 풀 수가 있습니다. 이 항은 흔히 regularizer라고 부르는데, $p(z)$를 표현하기 위해 $q(z|x)$를 사용하면 얼마나 많은 정보가 손실되는 지를 측정합니다. 쉽게 말해 $q(z|x)$가 $p(z)$에 얼마나 가까운지를 측정하는 measure라고 보시면 되겠습니다.

한편, (2)식의 의 RHS에서 두 번째 항인 도 어디서 많이 본 것 같은 모양입니다. 이 항은 (negative) reconstruction loss라고 부르는데, 얼마나 출력값이 입력값을 잘 따라가는 지를 측정합니다.

MNIST 같은 image 데이터를 사용한다면, ($p(x|z)$는 Bernoulli 분포, $q(z|x)$는 Gaussian 분포라고 가정하고) reconstruction loss를 입출력 image간의 binary cross-entropy로 계산할 수 있습니다. Binary cross-entropy를 수식대로 계산할 수도 있지만 Keras에서는 함수로 제공하기도 합니다.

정리하자면, 는 아래와 같이 쉽게 계산됩니다. (주의: gradient-descent로 계산하기 위해 부호가 반대로 바뀌었습니다.) 이 코드는 Agustinus Kristiadi의 블로그에서 인용했습니다.

def vae_loss(y_true, y_pred):
    """ Calculate loss = reconstruction loss + KL loss for each data in minibatch """
    # E[log P(X|z)]
    recon = K.sum(K.binary_crossentropy(y_pred, y_true), axis=1)
    # D_KL(Q(z|X) || P(z|X)); calculate in closed form as both dist. are Gaussian
    kl = 0.5 * K.sum(K.exp(log_sigma) + K.square(mu) - 1. - log_sigma, axis=1)

    return recon + kl

전체 VAE의 계산 알고리즘은 아래와 같습니다.

kingma-pp20

다음은 MNIST 대상의 실험 결과를 보여주는 동영상들입니다.

VAE에 대한 평가

지금까지 VAE는 아래와 같은 평가를 받고 있습니다. 주로 GAN과 비교되는 것은 어쩔 수가 없는 것 같습니다.

  • 장점
    • Log-likelihood를 통해 model의 quality를 평가할 수 있다.
    • 빠르고 training이 쉽다.
    • Loss 값을 계산할 수 있다.
  • 단점
    • 결과물의 quality가 떨어진다(blurry하다).
    • $q$가 optimal하더라도 $p$와 같지 않을 수도 있다.

(추가) 아래는 Company.AI 최정원 님의 자료에서 가져온 비교표입니다. 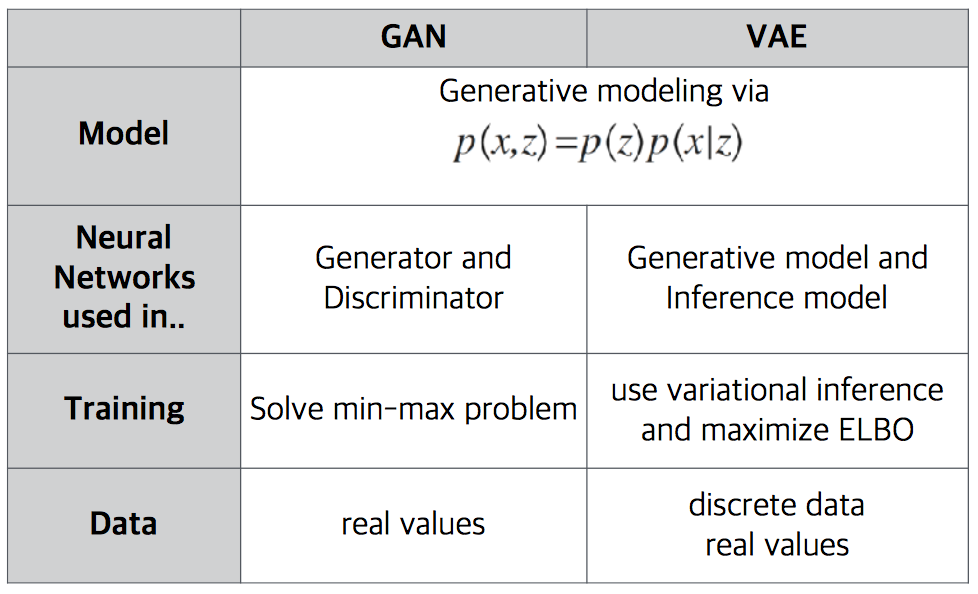choi-comparison

후속 연구로 이 논문의 저자들은 VAE를 classification 문제로 확장해 semi-supervised learning에 적용하는 논문 “Semi-Supervised Learning with Deep Generative Models”(NIPS '14)을 냈습니다. 또한, 최근 가장 많이 사용되는 optimizer인 Adam을 2015년에 발표하기도 했습니다. 이 논문들에 대해서는 나중에 다른 post에서 소개 드리겠습니다.

– Jamie;



References

Related Posts

Copyright © Jiyang "Jamie" Kang (강지양) and Pull Requests to Tomorrow, 2017. All rights reserved.